RAZONES TRIGONOMÉTRICAS

Las razones trigonométricas de un ángulo α son las razones obtenidas entre los tres lados de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c.

Sea α uno de los ángulos agudos del triángulo rectángulo.

El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c).

El coseno se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).

La tangente es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).

Razones trigonométricas de ángulos característicos

El seno, coseno y tangente de los ángulos más característicos (0º, 30º, 45º, 60º, 90º, 180º y 270º) son: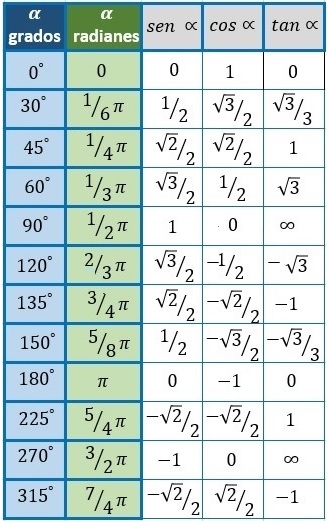

Razones trigonométricas recíprocas

Las razones trigonométricas recíprocas son los inversos multiplicativos de las razones  trigonométricas. Éstas son:

Cosecante (csc): es la razón recíproca del seno. Es decir, csc α · sen α=1.

Secante (sec): la razón recíproca del coseno. Es decir, sec α · cos α=1

Cotangente (cot): es la razón recíproca de la tangente. También en este caso, cot α · tan α=1

            Definición de las razones trigonométricas recíprocas

Las razones trigonométricas recíprocas de un ángulo α se obtienen como razones entre los tres lados de un triángulo rectángulo, siendo α uno de sus ángulos agudos.

• Cosecante de α. Se define como la razón entre la hipotenusa (c) y el cateto opuesto (a):
  
• Secante de α. Se define como la razón entre la hipotenusa (c) y el cateto contiguo o cateto adyacente (b):
  


Cotangente de α. Se define como la razón entre el cateto contiguo o cateto adyacente (b) y el cateto opuesto (a):

Razones trigonométricas recíprocas de ángulos característicos
Las razones trigonométricas recíprocas de los ángulos más característicos (0º, 30º, 45º, 60º, 90º, 180º y 270º) son:

Relación entre razones trigonométricas

Cualquier razón trigonométrica se puede expresar en función de cualquier otra. En la siguiente tabla se puede ver la fórmula con la que se expresa cada una en función de la otra.Nota: El signo ± que corresponde en cada caso depende del cuadrante en que esté el ángulo.